HARP GUI
The easiest way to use HARP is to download the latest stand-alone installers created for Mac or Windows. Run the installer, follow those instructions, then launch HARP.
Mac security issue. If you try to install on a Mac, you may encounter a security issue that won’t allow you to launch HARP because the OS cannot verify that it isn’t malware. You need to do the following:
- Go to the
Applemenu item - Open
System Settings - Go to the
Privacy & Securitytab on the side. - Scroll down past the
Privacysection, and into theSecuritysection - Find the section that says
HARP was blocked from use becasue it is not from an identified developer. - Click
Open Anyway
Using the HARP GUI
There are two modes that you can use within the HARP GUI. One is to download and process structures already posted to the PDB (i.e., the “PDB ID” tab), and the other is to load and process .cif and .map/.mrc files that you have on your computer (i.e., the “Files” tab). The third “Options” tab contains all the settings that are common to both modes. If you are trying to process your own unreleased structures, you should use the “Files” tab.
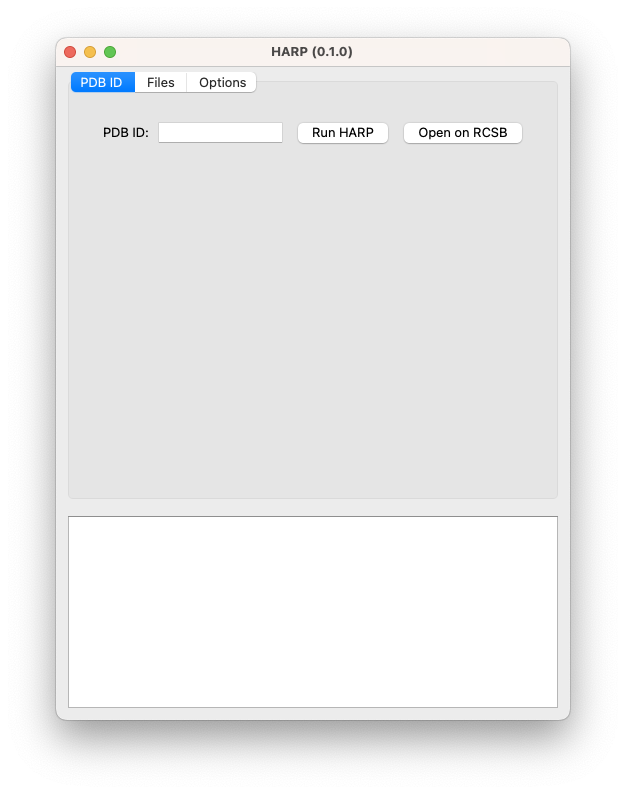
“PDB ID mode
With this mode, you can specifiy the PDB ID in the text box, and then run HARP or open the corresponding page on the RCSB. Downloading uses FTP access to the RCSB and currently only works on Mac. Files are downloaded into the “Working Directory” specified on the “Options” tab.
“Files” mode
With this mode, you can specify a model (mmCIF format in .cif or .cif.gz) and a map (MRC format, i.e., .map, .mrc; can be gzipped), and then run HARP. Currently, this has been tested using CryoSPARC created maps and PHENIX created models. 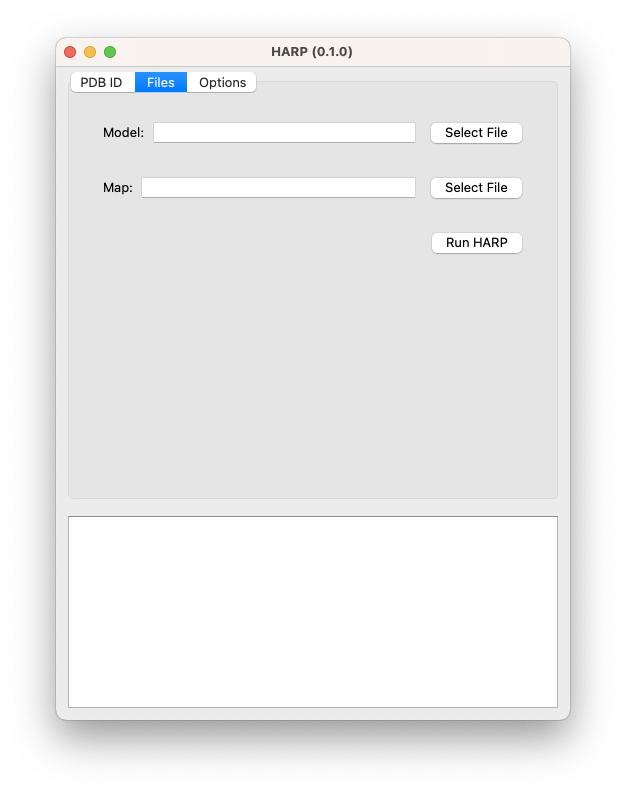
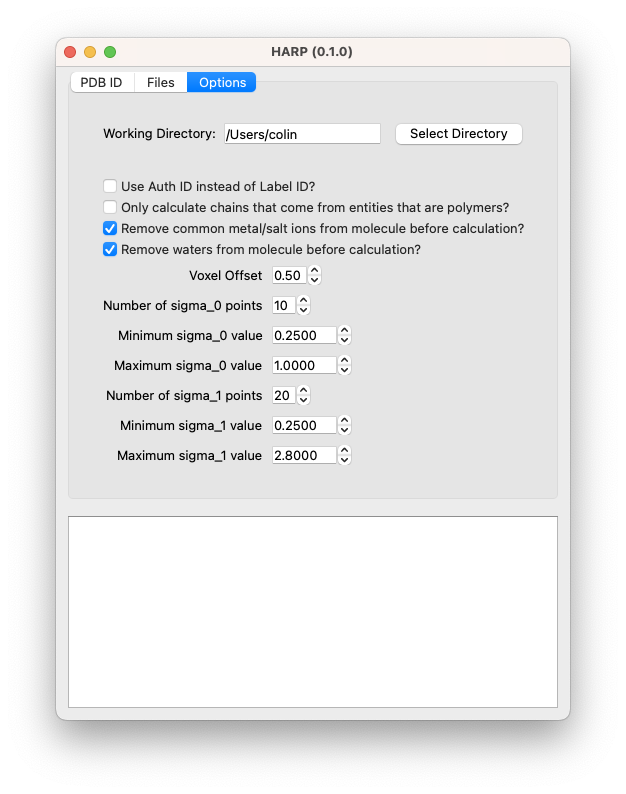
Options
- Working Directory: All files are saved here
- Auth ID/Label ID: Change which name is used for each residue
- Only polymers: Ignore all small molecules
- Remove metals: Removes common ions
- Remove waters: Removes waters
- Voxel offset: face-centered (0.5; default) or edge-centered (0.0) voxels
- \(\sigma_0\) and \(\sigma_1\) parameters: For defining the Rayleigh criterion for \(M_0\) and \(M_1\) and marginalization conditions.